Partition Array Into K Subsequences
Given a sorted assortment(in ascending order), cheque if the array tin be split into 1 or more subsequences of length greater than equals to 3 such that every subsequence contains consecutive numbers.
Examples
Input:
arr[] = {ane,2,3,3,4,5}
Output:
true
Caption:
The array can be split into ii subsequences as,
sub1[] = {i, 2, 3}
sub2[] = {3, iv, 5}
Input:
arr[] = {Z1, ii, iii, 3, four, four, 5, 5}
Output:
true
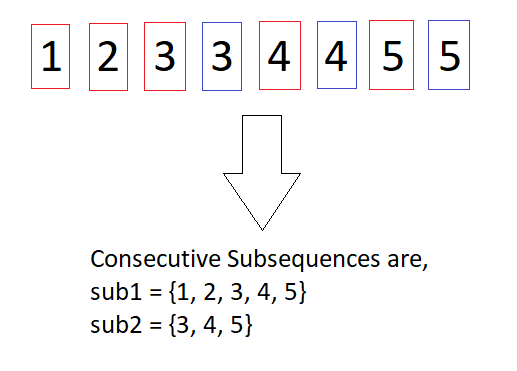
Explanation:
The consecutive subsequences are,
sub1[] = {1, 2, 3, iv, 5}
sub2[] = {three, iv, five}
Naive Approach for Split up Array Into Consecutive Subsequences
For an element arr[i] of the given array, it tin either form a new subsequence or can be added to a subsequence ending at (arr[i] – 1).
Information technology is e'er ameliorate non to form a new subsequence as forming a new subsequence may result in some subsequences of length less than iii. If at that place is no subsequence ending at (arr[i] – one), there is no option merely to form a new subsequence.
If in that location are more than than i subsequences that can accommodate the current element, always add the current element to the subsequence with the to the lowest degree number of elements, this will ensure the minimization of subsequences of length less than 3.
Algorithm
- The get-go element of the assortment always forms a new subsequence.
- Traverse the array starting from alphabetize 1(0 based indexing).
- Check if there is some subsequence that can arrange the current element, an chemical element arr[i] tin exist added to a subsequence ending at (arr[i] – 1).
- If there is no subsequence that can suit the current element course a new subsequence.
- Else choose the subsequence with a minimum size that can accommodate the current element and add the current chemical element to the called subsequence.
- After traversing the array, check if there is some subsequence of length less than iii, if aye, return false, else return true.
Java Code for Split Array Into Consecutive Subsequences
import coffee.util.ArrayList; public class SplitTheArrayIntoConsecutievSubsequences { private static boolean isPossible(int[] arr) { // If the lenght of arr is less than three, it is not possible to split the array if (arr == null || arr.length < three) { render faux; } int north = arr.length; // List of subsequences ArrayList<ArrayList<Integer>> al = new ArrayList<>(); // Starting time element always forms a new subsequence ArrayList<Integer> eles = new ArrayList<Integer>(); eles.add(arr[0]); al.add together(eles); // Traverse the array starting from index i for (int i = 1; i < n; i++) { // Required position of subsequence that can arrange the electric current element int pos = -1; // Size of required subsequence int size = -one; // Check if in that location is some subsequence that can arrange the electric current chemical element for (int j = 0; j < al.size(); j++) { // A subsequence ending at (arr[i] - 1) tin can conform the element arr[i] if (al.get(j).become(al.get(j).size() - 1) + 1 == arr[i]) { if (pos == -1) { pos = j; size = al.go(j).size(); } else { // Select the subsequence with minimum size if (al.get(j).size() < size) { pos = j; size = al.get(j).size(); } } } } // If at that place is no subsequence that can accommodate the current element // form a new subsequence if (pos == -1) { ArrayList<Integer> newAL = new ArrayList<>(); newAL.add(arr[i]); al.add(newAL); } else { // else add information technology to the required subsequence al.go(pos).add(arr[i]); } } for (int i = 0; i < al.size(); i++) { // if there is some subsequence of length less than 3, return imitation if (al.get(i).size() < 3) { return false; } } // No subsequence of length less than 3, return true return true; } public static void principal(String[] args) { // Instance 1 int arr1[] = new int[]{ane, two, 3, three, 4, 5}; Organization.out.println(isPossible(arr1)); // Instance 2 int arr2[] = new int[]{1, 2, 3, 3, 4, 4, 5, 5}; System.out.println(isPossible(arr2)); // Example 3 int arr3[] = new int[]{1, ii, three, 4, 4, 5}; System.out.println(isPossible(arr3)); } } true true false
C++ Code for Split Assortment Into Sequent Subsequences
#include<bits/stdc++.h> using namespace std; bool isPossible(int *arr, int northward) { if (n < 3) { return simulated; } // List of subsequences vector<vector<int>> v; // Kickoff element ever forms a new subsequence vector<int> eles; eles.push_back(arr[0]); v.push_back(eles); // Traverse the assortment starting from alphabetize 1 for (int i = 1; i < n; i++) { // Required position of subsequence that tin can conform the current element int pos = -1; // Size of required subsequence int size = -1; // Check if there is some subsequence that can adjust the current chemical element for (int j = 0; j < v.size(); j++) { // A subsequence ending at (arr[i] - 1) can accommodate the element arr[i] if (v[j][5[j].size() - one] + 1 == arr[i]) { if (pos == -1) { pos = j; size = five[j].size(); } else { // Select the subsequence with minimum size if (5[j].size() < size) { size = v[j].size(); pos = j; } } } } // If in that location is no subsequence that can adapt the current element // form a new subsequence if (pos == -1) { vector<int> newV; newV.push_back(arr[i]); five.push_back(newV); } else { v[pos].push_back(arr[i]); } } for (int i = 0; i < v.size(); i++) { if (v[i].size() < 3) { return fake; } } return true; } int chief() { // Example one int arr1[] = {1, two, 3, 3, four, 5}; if(isPossible(arr1, sizeof(arr1) / sizeof(arr1[0]))) { cout<<"truthful"<<endl; } else { cout<<"false"<<endl; } // Case 2 int arr2[] = {1, 2, 3, three, 4, iv, v, 5}; if (isPossible(arr2, sizeof(arr2) / sizeof(arr2[0]))) { cout<<"truthful"<<endl; } else { cout<<"faux"<<endl; } // Instance 3 int arr3[] = {1, 2, iii, four, 4, 5}; if (isPossible(arr3, sizeof(arr3) / sizeof(arr3[0]))) { cout<<"true"<<endl; } else { cout<<"imitation"<<endl; } render 0; } truthful true false
Complication Analysis
Time Complication = O(nii)
Space Complication = O(northward)
Optimal Approach for Split up Assortment Into Consecutive Subsequences
For an element arr[i], either it can class a new subsequence or can exist added to another subsequence catastrophe at (arr[i] – i), if there are more than one subsequence that can accommodate arr[i], add information technology to the subsequence of minimum length.
But 3 types of subsequence length are important, that is, subsequences of length 1, length 2 and length greater than equals to three, denoted every bit p1, c1, p2, c2, p3 and c3, where p ways previous and c means current.
For every number first count the number of occurrences of it in the array, bank check if it can spread across all the subsequences of length 1 and ii, if it cannot, return false immediately, because if the electric current number cannot extend subsequences of length 1 or 2, no number will practice as the array is sorted. Then there will remain some subsequences of length 1 or 2 at the end.
Else all the subsequences of length 1 converts to subsequences of length two, length two converts to length three, and remaining elements are added to subsequences of length 3 or more, if nevertheless some elements are not distributed they contributes to subsequences of length 1, else only the elements contributing to length iii or more adds to the new length three subsequences.
At the cease, if there are no length 1 and length 2 subsequences return truthful, else return false.
Java Code
public class SplitArrayIntoConsecutiveSubsequences { private static boolean isPossible(int[] arr) { int n = arr.length; if (n < 3) { render false; } int p1 = 0, p2 = 0, p3 = 0; int c1 = 0, c2 = 0, c3 = 0; int i = 0; // prev denotes previous element // curr denotes current element int prev = 0, curr = 0; // Traverse the array while (i < northward) { // Electric current becomes previous p1 = c1; p2 = c2; p3 = c3; prev = curr; curr = arr[i]; int count = 0; // Count the frequency of current chemical element while (i < northward && arr[i] == curr) { i++; count++; } if (prev + one == curr) { // if chemical element cannot be spread across subsequences of length 1 and 2 if (count < p1 + p2) { // return false immediately return simulated; } // Update c1, c2, c3 as described c1 = Math.max(0, count - (p1 + p2 + p3)); c2 = p1; c3 = p2 + Math.min(p3, count - (p1 + p2)); } else { // this element cannot exist spread across any subsequence if (p1 != 0 || p2 != 0) { // if there is any subsequence of length i or 2 // return simulated immediately return false; } // Update c1, c2, c3 as described c1 = count; c2 = 0; c3 = 0; } } // if in that location are no length 1 and length ii subsequences return true, else return fake render (c1 == 0 && c2 == 0); } public static void main(String[] args) { // Example one int arr1[] = new int[]{1, 2, 3, three, 4, 5}; Arrangement.out.println(isPossible(arr1)); // Example ii int arr2[] = new int[]{one, 2, three, 3, 4, 4, 5, v}; System.out.println(isPossible(arr2)); // Example three int arr3[] = new int[]{1, 2, three, iv, 4, 5}; System.out.println(isPossible(arr3)); } } true true false
C++ Code
#include<bits/stdc++.h> using namespace std; bool isPossible(int *arr, int n) { if (n < three) { return false; } int p1 = 0, p2 = 0, p3 = 0; int c1 = 0, c2 = 0, c3 = 0; int i = 0; // prev denotes previous element // curr denotes electric current element int prev = 0, curr = 0; // Traverse the array while (i < n) { // Current becomes previous p1 = c1; p2 = c2; p3 = c3; prev = curr; curr = arr[i]; int count = 0; // Count the frequency of current element while (i < n && arr[i] == curr) { i++; count++; } if (prev + 1 == curr) { // if chemical element cannot be spread beyond subsequences of length 1 and ii if (count < p1 + p2) { // return false immediately return false; } // Update c1, c2, c3 as described c1 = std::max(0, count - (p1 + p2 + p3)); c2 = p1; c3 = p2 + std::min(p3, count - (p1 + p2)); } else { // this element cannot be spread across whatsoever subsequence if (p1 != 0 || p2 != 0) { // if there is any subsequence of length 1 or 2 // render false immediately render false; } // Update c1, c2, c3 every bit described c1 = count; c2 = 0; c3 = 0; } } // if there are no length 1 and length 2 subsequences return true, else return false render (c1 == 0 && c2 == 0); } int main() { // Case i int arr1[] = {ane, 2, 3, 3, 4, 5}; if(isPossible(arr1, sizeof(arr1) / sizeof(arr1[0]))) { cout<<"true"<<endl; } else { cout<<"simulated"<<endl; } // Example two int arr2[] = {1, 2, three, 3, four, 4, v, 5}; if (isPossible(arr2, sizeof(arr2) / sizeof(arr2[0]))) { cout<<"truthful"<<endl; } else { cout<<"false"<<endl; } // Instance 3 int arr3[] = {ane, 2, iii, 4, 4, five}; if (isPossible(arr3, sizeof(arr3) / sizeof(arr3[0]))) { cout<<"true"<<endl; } else { cout<<"false"<<endl; } render 0; } true true false
Complexity Analysis
Fourth dimension Complexity = O(north)
Infinite Complication = O(1)
References
Partition Array Into K Subsequences,
Source: https://www.tutorialcup.com/interview/array/split-array-into-consecutive-subsequences.htm
Posted by: moorehicave.blogspot.com


0 Response to "Partition Array Into K Subsequences"
Post a Comment